MatrixGrader #
MatrixGrader is an extended version of FormulaGrader used to grade mathematical expressions containing scalars, vectors, and matrices. Authors and students may enter matrix (or vector) expressions by using variables sampled from matrices, or by entering a matrix entry-by-entry.
Compared to FormulaGrader, MatrixGrader has enhanced error-handling capabilities specific to issues with arrays, extra functions for manipulating vectors and matrices, and partial credit options for component-by-component comparison.
Do not let its name fool you: MatrixGrader is capable of handling vectors, matrices and tensors. We will sometimes refer to all of these possibilities as "arrays" (MatrixGrader just sounds cooler than ArrayGrader though, doesn't it?).
A First Example #
A typical use of MatrixGrader might look like
>>> from mitxgraders import *
>>> grader1 = MatrixGrader(
... answers='4*A*B^2*v',
... variables=['A', 'B', 'v'],
... identity_dim=2, # makes 'I' available to students as the 2x2 identity matrix
... sample_from={
... 'A': RealMatrices(), # samples from 2 by 2 matrices by default
... 'B': RealMatrices(),
... 'v': RealVectors(shape=2), # sample 2-component vectors
... }
... )
The next few lines call the grader as a check function. The inputs '4*A*B^2*v' and '4*A*B*B*v' are correct:
>>> result = grader1(None, '4*A*B^2*v')
>>> result == {'grade_decimal': 1, 'msg': '', 'ok': True}
True
>>> result = grader1(None, '4*A*B*B*v')
>>> result == {'grade_decimal': 1, 'msg': '', 'ok': True}
True
while the input '4*B*A*B*v' is incorrect because the matrix-sampled variables are non-commutative:
>>> result = grader1(None, '4*B*A*B*v')
>>> result == {'msg': '', 'grade_decimal': 0, 'ok': False}
True
Matrix Sampling #
In the MatrixGrader example above, the variables A and B were sampled from RealMatrices(). The RealMatrices sampling class samples from 2 by 2 matrices by default but can be configured to sample matrices of different shapes. See Sampling for more information about matrix and vector sampling.
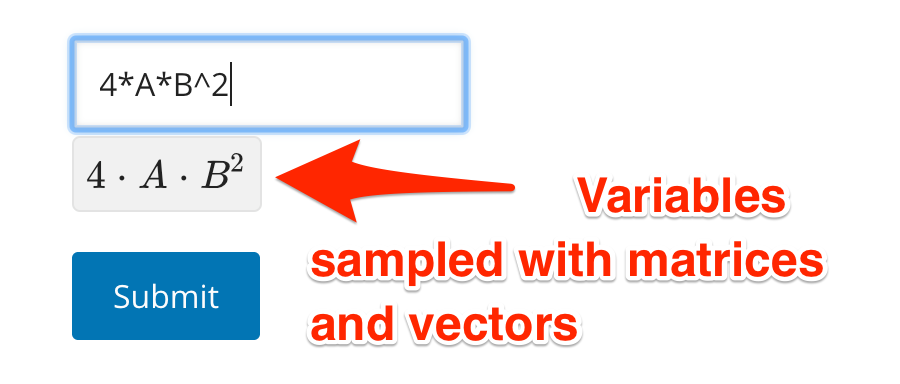
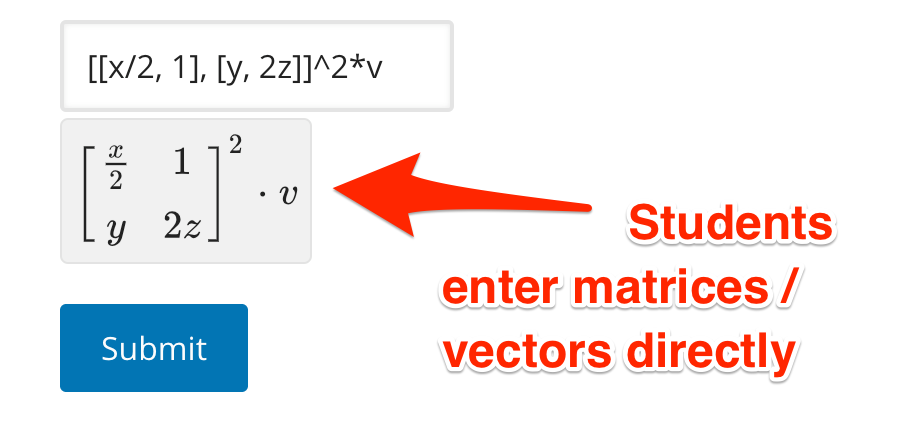
Matrix Entry #
In addition to using variables that vectors and matrices, students can also enter matrices and vectors directly, entry-by-entry.
| Input with symbols: | Input entry-by-entry: |
|---|---|
 |
 |
Note
- In order for matrices entered entry-by-entry to display correctly in edX, authors must use the AsciiMath renderer provided by
<textline math='true'/>.
By default, students can only input vectors and not matrices. This is configured through the max_array_dim configuration key:
max_array_dim=1: This (the default) allows students to enter vectors entry-by-entry but not matrices.- entering vector
[x, y + 1, z]is OK. - entering matrix
[[1, x], [y, 2]]raises an error.
- entering vector
max_array_dim=2: This allows student to vectors and matrices.- entering vector
[x, y + 1, z]is OK. - entering matrix
[[1, x], [y, 2]]is OK. - entering tensor
[ [[1, 2], [3, 4]], [[5, 6], [7, 8]] ]raises an error.
- entering vector
The decision to disable matrix-entry by default is intended to prevent students from entering single-row or single-column matrices when a vector is expected.
Matrix Operations and MathArrays #
MatrixGrader uses a custom subclass of numpy.ndarray to internally represent matrices. Understanding how the MathArray class behaves is useful for creating MatrixGrader problems, and MathArray can be used directly by problem-authors to add extra matrices to a problem.
How MatrixGrader uses MathArrays #
Whether a matrix is input entry-by-entry or represented through variables, MathArrays are used to evaluate student expressions.
For example, consider the grader below.
>>> grader = MatrixGrader(
... answers='2*A*[1, 2, 3] + v',
... user_constants={
... 'A': MathArray([[1, 2, 3], [4, 5, 6]])
... },
... variables=['v'],
... sample_from={
... 'v': RealVectors(shape=2) # samples a random 2-component vector
... }
... )
When a student inputs v + A*2*[1, 2, 3] to the grader above, a calculation similar to
>>> v = MathArray([2, -1]) # Really, random samples would be chosen.
>>> A = MathArray([[1, 2, 3], [4, 5, 6]])
>>> v + A*2*MathArray([1, 2, 3]) # below is the result of evaluating student input, which would next be compared to author's answer
MathArray([30, 63])
is performed (but repeated multiple times with different values for the random variables).
Dimension and Shape #
MathArrays have dimension and shape. For example:
| Student Input | Converted to | Name | dimension | shape |
|---|---|---|---|---|
[1, 2, 3] |
MathArray([1, 2, 3]) |
"vector" | 1 |
(3, ) |
[[1, 2, 3], [4, 5, 6]] |
MathArray([[1, 2, 3], [4, 5, 6]]) |
"matrix" | 2 |
(2, 3) |
[[1, 2, 3]] |
MathArray([[1, 2, 3]]) |
"single-row matrix" | 2 |
(1, 3) |
[[1], [2], [3]] |
MathArray([[1], [2], [3]]) |
"single-column matrix" | 2 |
(3, 1) |
[[[1, 2]], [[3, 4]]] |
MathArray([[[1, 2]], [[3, 4]]]) |
"tensor" | 3 |
(1, 1, 2) |
Tensor math arrays (dimension 3+) currently have very little support.
Warning
Note that a vector, a single-column matrix, and a single-row matrix are distinct entities. We suggest avoiding single-row and single-column matrices.
Allowed operations #
MathArrays support the usual binary operations for vectors and matrices, with appropriate shape restrictions. Compared to numpy.ndarray, MathArray has much more stringent shape restrictions.
-
Addition and Subtraction: Performed elementwise.
Expression raises error unless result type MathArray +/- MathArrayboth inputs have exactly the same shape MathArrayMathArray +/- numbernumber=0MathArraynumber +/- MathArraynumber=0MathArray -
Multiplication: Note that
vector * vectoris a dot productExpression left-input shape right-input shape raises error unless result type vector * vector(k1, )(k2, )k1=k2number(dot product of two vectors)MathArray * numberany - - MathArray(elementwise multiplication)number * MathArray- any - MathArray(elementwise multiplication)matrix * vector(m, n)(k)n=kvectorwithmcomponentsvector * matrix(k, )(m, n)m=kvectorwithncomponentsmatrix * matrix(m1, n1)(m2, n2)n1=m2matrixof shape(m1, n2)Note: Matrix multiplication may give students "too much power" for the type of problem you're asking. For example, if you want students to enter the product of two matrices or dot product of two vectors, you don't want them just entering the two quantities with a
*between them. You can disable multiplication in MatrixGrader problems by settingforbidden_strings=['*']. -
Division: Division either raises an error, or is performed elementwise:
Expression raises error unless result type any / MathArrayalways raises error - MathArray / number- MathArray(elementwise division) -
Powers: If
Ais a MathArray, thenA^kwill always raise an error unlessAis a square matrix, andkis an integer.
In this case,
A^kis equivalent to:krepeated multiplications ofAifk > 0,(inverse of A)^|k|ifk < 0, and- the identity matrix if
k=0.
Note: Negative exponents can give students "too much power". For example, if you want students to enter the inverse of
[[1, 2], [3, 4]], you probably want them to enter[[-2, 1], [1.5, -0.5]]rather than[[1, 2], [3, 4]]^-1. To this end, you can disable negative powers in MatrixGrader problems by settingnegative_powers=False.
A Note About Vectors #
Vectors are distinct from single-row matrices and single-column matrices, and can be left- or right-multiplied by a matrix:
>>> vec = MathArray([1, 2, 3])
>>> row = MathArray([[1, 2, 3]])
>>> col = MathArray([[1], [2], [3]])
>>> try:
... vec + row # raises error
... except StudentFacingError as error:
... print(error)
Cannot add/subtract a vector of length 3 with a matrix of shape (rows: 1, cols: 3).
>>> A = MathArray([[1, 2, 3], [4, 5, 6]])
>>> A * vec # matrix * vector
MathArray([14, 32])
>>> other_vec = MathArray([1, 2])
>>> other_vec * A # vector * matrix
MathArray([ 9, 12, 15])
We suggest avoiding single-column and single-row matrices.
Shape Errors #
When operations cannot be performed because of shape-mismatch, MathArray raises readable StudentFacingErrors. These error messages are intended to be presented directly to students. For example:
>>> A = MathArray([[1, 2], [3, 4], [5, 6]]) # matrix, shape (3, 2)
>>> B = MathArray([[1, 2], [3, 4]]) # matrix, shape (2, 2)
>>> v = MathArray([1, 2]) # vector, shape (2, )
Some sample error messages:
| Student input: | Valid? | Student receives error message: |
|---|---|---|
'A+B' |
No | Cannot add/subtract a matrix of shape (rows: 3, cols: 2) with a matrix of shape (rows: 2, cols: 2). |
'v*A' |
No | Cannot multiply a vector of length 2 with a matrix of shape (rows: 3, cols: 2). |
'B*v' |
Yes | |
'A^2' |
No | Cannot raise a non-square matrix to powers. |
'B^2' |
Yes |
Handling Errors #
While grading a student's input, matrix-related errors can occur in three places:
- while parsing the student's input,
- while evaluating the student's input, and
- while comparing the student's input to the author's stored answer.
Parse Errors: #
For example, if a student enters '[[1, 2],[3] ]', a matrix missing an entry in second row:
>>> grader = MatrixGrader(
... answers='[[1, 2], [3, 4]]',
... max_array_dim=2, # allow students to enter matrices entry-by-entry
... )
>>> student_input = '[[1, 2], [3]]'
>>> try:
... grader(None, student_input) # grade the input like edX would
... except StudentFacingError as error:
... print(error) # students see this error message
Unable to parse vector/matrix. If you're trying to enter a matrix, this is most likely caused by an unequal number of elements in each row.
Such parse errors are always displayed to students.
Shape-Mismatch Errors During Evaluation #
If a student submits an answer that will raise shape-mismatch errors then an error is raised with a helpful message. This avoids consuming one of the student's attempts. For example:
>>> grader = MatrixGrader(
... answers='[11, 22, 33]',
... )
>>> student_input = '[10, 20, 30] + [1, 2]' # Error! Adding vectors with different shapes
>>> try:
... grader(None, student_input) # grade the input like edX would
... except StudentFacingError as error:
... print(error) # students see this error message
Cannot add/subtract a vector of length 3 with a vector of length 2.
If you would rather mark the student incorrect when shape errors occur (and also consume an attempt), set shape_errors=False.
Shape-Mismatch Errors During Comparison #
If the author's answer is a 3-component vector, and the student submits a different 3-component vector, then they will be marked incorrect. However, if the student submits a 2-component vector or a number, they will receive an error message:
>>> grader = MatrixGrader(
... answers='[1, 2, 3]',
... )
>>> student_input = '[1, 2, -3]' # wrong answer
>>> result = grader(None, student_input) # grade the input like edX would
>>> result == {'msg': '', 'grade_decimal': 0, 'ok': False}
True
>>> student_input = '[1, 2, 3, 4]' # too many components
>>> try:
... grader(None, student_input) # grade the input like edX would
... except StudentFacingError as error:
... print(error) # students see this error message
Expected answer to be a vector, but input is a vector of incorrect shape
>>> student_input = '0' # scalar; should be a vector
>>> try:
... grader(None, student_input) # grade the input like edX would
... except StudentFacingError as error:
... print(error) # students see this error message
Expected answer to be a vector, but input is a scalar
The default handling of shape errors that arise when comparing student input to author's answer is:
- raise an error (do not mark student incorrect), and
- reveal the desired type (above, a vector) but not the desired shape (above, 3-components)
This behavior can be configured through the answer_shape_mismatch key. We can choose whether an error is presented or an attempt is consumed through the is_raised key, while we choose whether to reveal the desired input shape or type with the msg_detail key. For example, to
- mark students wrong instead of raising an error, and
- reveal the shape and the type
we can use:
>>> grader = MatrixGrader(
... answers='[1, 2, 3]',
... answer_shape_mismatch={
... 'is_raised': False,
... 'msg_detail': 'shape' # must be one of: None, 'type', 'shape'
... }
... )
>>> student_input = '0' # wrong shape
>>> result = grader(None, student_input) # grades the input like edX would
>>> result == {
... 'grade_decimal': 0,
... 'msg': 'Expected answer to be a vector of length 3, but input is a scalar',
... 'ok': False
... }
True
Hiding All Error Messages #
MatrixGraders can be used to introduce non-commuting variables. In such a situation, students may not know that the variables they are using are matrices "under the hood", and so we want to suppress all matrix errors and messages. We can do this by setting suppress_matrix_messages=True, which overrides answer_shape_mismatch={'is_raised'} and shape_errors. In the following example, A and B are secretly matrices that don't commute, but students will never see a matrix error message from typing something like 1+A.
>>> grader = MatrixGrader(
... answers='A*B',
... variables=['A', 'B'],
... sample_from={
... 'A': RealMatrices(),
... 'B': RealMatrices()
... },
... max_array_dim=0,
... suppress_matrix_messages=True
... )
>>> grader(None, 'A*B')['ok']
True
>>> grader(None, 'B*A')['ok']
False
>>> grader(None, 'A+1')['ok']
False
Note that this will also suppress error messages from trying to do things like sin([1, 2]) or [1, 2]^2. If your answer needs to take functions of the non-commuting variables, then this option is insufficient.
Matrix Functions #
MatrixGrader provides all the default functions of FormulaGrader (sin, cos, etc.) plus some extras such as trans(A) (transpose) and det(A) (determinant). See Mathematical Functions for full list.
Since MatrixGrader has all of FormulaGrader's configuration options, additional functions can be supplied through the user_functions configuration key. If you supply additional matrix functions, you may wish you use the specify_domain decorator function to provide meaningful error messages to students. See User Functions for details.
Identity Matrix #
To make an nxn identity matrix available to students, specify the configuration key identity_dim=n. That is, the grader MatrixGrader(identity_dim=4, ...) will automatically have a constant I whose value is the 4 by 4 identity matrix.
If you want a different name (besides I) for the identity, or if you encounter situations where identity matrices of different sizes are required, you can use the identity function. For example:
>>> grader = MatrixGrader(
... answers='[1, 2, 3]',
... user_constants={
... 'I_2': identity(2), # the 2 by 2 identity
... 'I_3': identity(3) # the 3 by 3 identity
... }
... )
Partial Credit #
A special comparer called MatrixEntryComparer has been built to cater for partial credit in MatrixGrader problems. In order to facilitate the use of MatrixEntryComparer, if either of the following two configuration options are present, MatrixGrader will use MatrixEntryComparer as the default comparer instead of equality_comparer.
entry_partial_credit:proportionalor a numberentry_partial_msg: The message to display
See the documentation for MatrixEntryComparer for details on how these options work.
Configuration Options #
MatrixGrader has almost all of FormulaGrader's configuration options, plus some extras. The extras are:
identity_dim: If specified as a positive integern, then an n by n identity matrix is added to the available constants with name'I'. Defaults toNone.max_array_dim(nonnegative int): Controls the maximum dimension of arrays that students can enter entry-by-entry. Default is1: vectors can be entered entry-by-entry, but not matrices.negative_powers(bool): whether negative powers are enabled for square matrices (which calculate powers of matrix inverse). Defaults toTrue.shape_errors(bool): See Handling Errors: Shape-mismatch errors during evaluation. Defaults toTrue.suppress_matrix_messages(bool): See Hiding All Error Messages. Defaults toFalse.-
answer_shape_mismatch(dict): A dictionary whose keys are listed below. Some or all keys may be set. Unset keys take default values. See Handling Errors: Shape-mismatch errors during comparison for details.'is_raised'(bool): defaults toTrue'msg_detail'(None | 'type' | 'shape'): defaults to'type'
-
entry_partial_credit: If set toproportionalor a number, uses this setting withMatrixEntryCompareras the default comparer. entry_partial_msg: If set to a text value, uses this setting withMatrixEntryCompareras the default comparer.
The FormulaGrader configuration keys that MatrixGrader does not have are:
allow_inf: We are unable to handle infinities appearing in vectors/matrices.